中科大-凸优化 笔记（lec47）-最速下降法
本文共 520 字，大约阅读时间需要 1 分钟。
全部笔记的汇总贴（视频也有传送门）：
一、梯度下降法
d k + 1 = − ∇ f ( x k ) f ( x k + 1 ) − P ∗ f ( x k ) − P ∗ ≤ 1 − m M ≤ 1 − min { 2 m γ α m a x , 2 m γ β M } K ∼ log ( f ( x k ) − P ∗ ) 线 性 收 敛 d^{k+1}=-\nabla f(x^k)\\\frac{f(x^{k+1})-P^*}{f(x^k)-P^*}\le1-\frac mM\le1-\min\{2m\gamma\alpha_{max},\frac{2m\gamma\beta}M\}\\ K\sim \log(f(x^k)-P^*)\;\;\;\;\;线性收敛 dk+1=−∇f(xk)f(xk)−P∗f(xk+1)−P∗≤1−Mm≤1−min{ 2mγαmax,M2mγβ}K∼log(f(xk)−P∗)线性收敛
二、最速（陡）下降法
三、Gradient与Steepest Gradient的变种
1）坐标轮换法
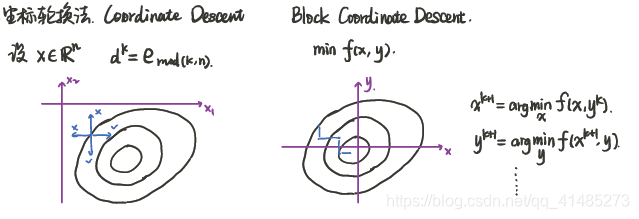
2）若 f ( x ) f(x) f(x)在某些点不可微
例：
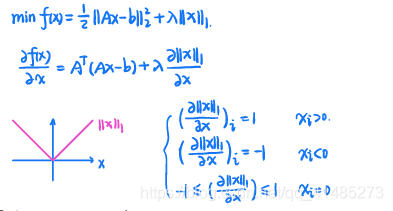
下一章传送门：
转载地址：http://aepq.baihongyu.com/
你可能感兴趣的文章
LeetCode 200.岛屿数量
查看>>
LintCode 178.图是否是树
查看>>
LintCode168.吹气球
查看>>
课程总结（第一周）
查看>>
【Java基础】 Java面向对象之抽象类、接口详解
查看>>
【IDEA系列】HelloWorld 项目创建及相关配置文件介绍
查看>>
我要偷偷的学C语言，然后惊呆所有人（第八天）
查看>>
关于LeetCode刷题及题目列表归纳
查看>>
【大数据Spark系列】Spark Transformation和Action算子
查看>>
【大数据Flink系列】Flink 核心概念综述
查看>>
【大数据Kafka系列】深入理解Kafka副本机制
查看>>
【Django系列】Django模板所有知识点总结
查看>>
【Java系列】Spring常见知识点
查看>>
wxPython中TextCtrl的输入上限问题
查看>>
Python进程间共享内存（版本3.8+）
查看>>
行为树 --- [1] BehaviorTree.CPP的编译及使用
查看>>
安装和使用google-perftools工具
查看>>
使用Python+yolov3实现对帧数不等长视频进行批处理
查看>>
Java队列Queue
查看>>
专业mac数据恢复软件Tenorshare UltData Mac
查看>>